Fractals have been touched upon previously regarding the Mandelbrot set, but here I want to introduce something a touch more simple. Imagine you have a square of card in front of you. Divide it into nine equal squares then punch out the central square. Now look at the remaining eight squares. Divide these into nine squares each, then punch out the central hole of each of these. Repeat this process again and again as your squares gradually get smaller then repeat this an infinite number of times. If you attempt this on a real piece of card you will find it soon becomes very difficult, or if you repeat as an animation, your initial square will soon seem to disappear. This is because your Sierpinski Carpet (the fractal was named after its founder in 1916) has no area, but does have an infinite perimeter. This is quite easy to see with only the smallest use of maths. Originally we had a square, we divided it into nine, then removed one of these nine (one ninth of the starting area) to leave eight squares (eight ninths of the starting area). We then repeat the process and take one ninth of all the remaining squares, so our square of one unit’s surface area was reduced to eight ninths of its size, and has been again. This repeats for every iteration you perform, and can be quite simply be written as
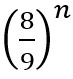
where n is the number of iterations carried out. I said above that we should carry this out an infinite number of times, and as your result gets smaller as n gets bigger, this tends to 0 as n tends to ∞. For each iteration the perimeter, on the other hand, has been increasing. For the first iteration we added four times a third of the original length of the square once, then we added four times a ninth of the original length eight times, then we added four times a twenty-seventh of the original length sixty-four times and so on, which can be summarised as below.
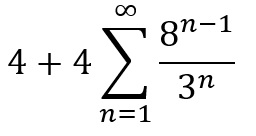
We can see that the numerator increases at a greater rate than the denominator, and so each consecutive term is larger, so both the terms and the overall sum tend to infinity.
This can be taken out of two dimensions as well. If we instead consider a cube, then divide it into 27 smaller cubes of equal dimensions to one another then punch the centre ones out as seen form each face so that there is a whole all of the way through the cube. As with the Sierpinski Carpet, we then repeat this process on the smaller cubes, and the process gradually produces the image below, a Menger Sponge.

This has the same properties as the Sierpinski Carpet, just in one higher dimension: the volume is equal to zero, and the surface area is infinite, and the same logic can be followed to deduce this, just with the volume changing by a factor of 20/27, and the surface area for each iteration is
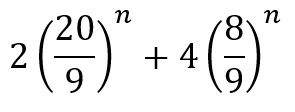
and again as n tends to infinity, so will the surface area. Unfortunately it is quite hard to define an object that has infinite surface area and no volume, so things get a bit weird. It isn’t a 3D object as it has no volume, and if someone described an object that had no volume to you, you would probably say it was not 3D, even if the illustration of the Menger Sponge seems to contradict that. If, however, you choose one particular spot and looked at it, it will just be full of infinitely many holes, so appear to have no area (though the maths says otherwise) so it isn’t described as a 2D object either, instead its topological dimension is a 1D curve.
Many exciting things can come out of the Menger Sponge. If you were to look along the Menger Sponge’s diagonal, then make a perpendicular cut halfway along this line you will get a hexagonal fractal with repeating hexagrams (which look like six pointed stars).

An even more exciting thing to get out of the Menger Sponge is pi. To explain this we have to start with the Sierpinski Carpet, as Ed Pegg, noted for being one of the first to do this, did. If you start with a square of 2 units by 2 units, divided into four smaller squares, you have a square of area 4 units squared. Now divide these four squares into 9 other squares and pop the central one out, then divide the resulting 32 squares not into 9 squares each but instead 25 squares and remove the centre square again. For each iteration the divisions on a length of one of the squares will increase by 2, so they will be an odd number in length, and that number squared for the area (3 and 9, then 5 and 25 above), as a proportion of the last iteration it will be the odd number squared minus one, divided by the odd number squared. Written more simply as
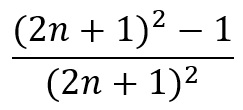
which will be 8/9 for the first iteration, then 24/25, then 48/49, then 80/81 and so on. Unlike a true Sierpinski Carpet the area of this does not tend to 0 as for each iteration the proportion of area removed decreases. Instead something far more exciting happens: the area tends towards pi! We can write the product as
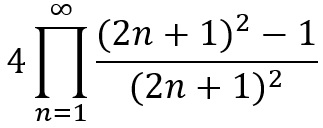
which equals pi (though if infinity’s too big for consideration, replacing it with 100,000,000 gives 3.1415). What other shapes have a distance of one from their centre to their outside edge? The circle of course, which may seem irrelevant, but comes up quite surprisingly with the Menger Sponge. If we repeat the above process in 3 dimensions (it is three dimensions this time as some volume remains) we get the product equation
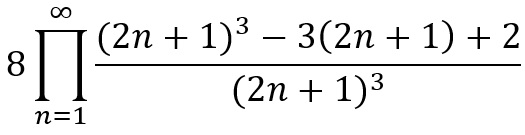
which gives 4π/3. Ring a bell? This is the volume of a sphere of radius one!
If this hasn’t all been quite exciting enough for you, you could instead make your own Menger Sponge. For the more casual mathematician you can visit http://megamenger.com/ to find the instructions for the construction of a first order Menger Sponge (mine is pictured below).

This was run by a group called Mega Menger who endeavoured to create a level 4 Menger Sponge distributed around the world, which meant creating 20 sponges (level 3) made of 20 smaller sponges (level 2), each made of 20 of the one pictured above (a level 1 sponge). A map of all the level 3 locations can be found on the Mega Menger website, but sites include the Cambridge University Maths Department, pictured badly below from my recent visit there; the University of Bath; Tampere, Finland; Almería, Spain; Dulwich International High School, Suzhou, China; and the Auckland Art Gallery, New Zealand.
Rather surprisingly of the great achievements of many of these institutions have produced, these level 3 Menger Sponges take pride of place in key areas of their buildings, for example in Cambridge it was only a few steps from the main door. So, if you want to do some not particularly taxing maths, remember even Cambridge maths students enjoy a bit of arts and crafts.
Update: Though the University of Bath did create a third order Menger Sponge it has since been destroyed due to irreparable wear and tear.

