The Königsberg Bridge Problem unsurprisingly originates from Konigsberg, nowadays Kaliningrad, which sits on the river Preger, formerly part of Germany, now a Russian city. In the river sat an island, and on one side the river forked. This gave four landmasses to consider, a north one, a south one, an easterly one, and the island itself. Seven bridges connected the area, two from the north to the island, two from the south to the island, one from the island to the east, one from the north to the east, and one from the south to the east, as shown: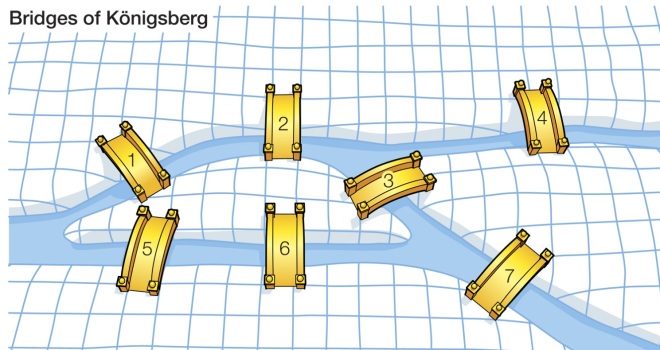
The problem was, can you start at a point, go over all the bridges once, and end up where you started. For a long time it was just a tradition of the town to see if you could completere the problem, but in 1736 Euler (previously mentioned regarding Euler’s Identity) decided to try to tackle the issue, and concluded it to be impossible by considering the problem without the context to create a “graph”, where each land mass was a vertex, and each bridge a connecting line, as below:

This was the start of graph theory, which is an area of mathematics nowadays, where a “graph” is defined as a collection of points and lines connecting some (possibly empty) subset of them (as opposed to a plotted graph, which shows a function of x), though the first deep investigation into it was by D. König in the 1930s, two centuries after Euler’s time. Concerning this problem the key characteristic considered was how many lines connected to each vertex, and odd number or an even number. If we look at the graph we see that all four have an odd number of lines going in. Now lets consider a point in isolation. If it has three lines going into it, what can you do? You can start at that point, leave, come back again then leave again, or you can start outside of it, enter it, leave it, then enter it and stay in it. As you increase the odd number, it increases by two, which just equates to leaving and re-entering another time.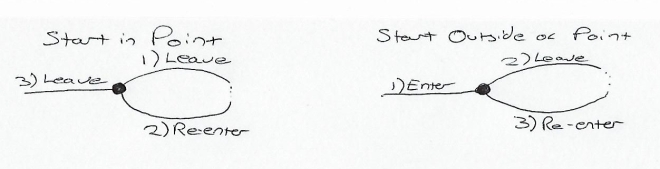
This shows that you either have to start in the point, or end up in the point, and if we consider a single path, there is only ever one starting point and one ending point, and so any graph which holds true to the problem must have either two or no odd vertices. You can only start or end in such a point as well, so if you wish to start and finish at the same point, there must be no odd vertices. We then look at our graph of Königsberg and see that it has four odd vertices, so by logic alone it can be shown that the problem is impossible, just as Euler had said. Nowadays such a route (going over every line once, and having the same start/finish point) is called an Eulerian Path.
Other problems to which graph theory can be applied include the classic fox, hen and grain problem. If you are a courier with three such items, a river to cross, and a boat with room for only you and one of the items, how do you get all three across if, when left unattended, the hen eats the grain, and the fox eats the hen. You could think about this for a while and come up with a solution, or you could turn it into a graph, where a vertex represents and animal, and a line marking what eats what.
To get them across, you need to ensure no lines remain, so the first logical step would be to take the hen. Drop that on the other side of the river, then come back and take one of the others over. Now, however you would have a line drawn on the other side of the river, so you have to take the hen back. Now there would be a line on the other side, so you take the non-hen item, drop that off, then you can pop back and grab the hen. You can expand this problem for any number of animals, and then see what size boat you would need to succeed in solving the puzzle.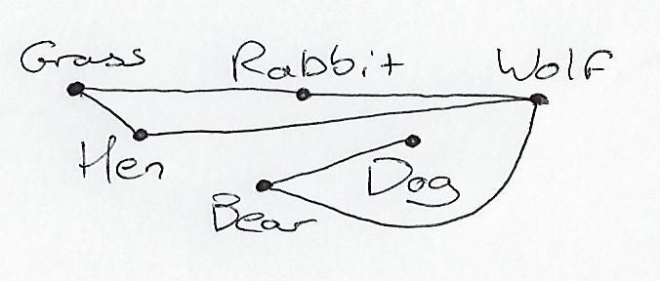
Hear we have a very hungry bear who eats dogs and wolves, a friendly dog that eats nothing, a wolf that eats rabbits and hens, and a rabbit and a hen that both eat grass. The number of spaces in the boat required would be three to take either the bear, rabbit and hen, or the dog, wolf and grass, then the boater would have to come back for the other three. This, though, can be applied to other combinations of items.
Königsberg got bombed during the Second World War and all of the bridges were lost, and only five rebuilt, changing the problem slightly.

Now we have a graph with two even vertices, and two odd ones. This means you still can’t end up in the same place after crossing every bridge, but you can cross every bridge once, as long as you start and finish in the two odd vertices.
Graph theory also led to Topology, which can be used for all sorts of things, particularly maps, so a final challenge, is there any underground system for which you can create an Eulerian Path?

